GIMPS User login ID: mikr

Introduction

I from Poland - mi.kr@interia.pl

Since March 8, 2013 I participate in project GIMPS (Great Internet Mersenne Prime Search)
So far (as of November 1, 2024) I found the Mersenne number 56,124 factors using three methods:

  • TF 54,054 factors;
  • P-1 1,800 factors (including 46 composite factors) Top500 list;
  • ECM 268 factors Here they are all;
  • P+1 – 2 factors Here they are list;

    • There is a link to all my factors - as at November 01, 2024 You can download the file PDF format (877 pages A4!).

    Below is the opening excerpt of this file:


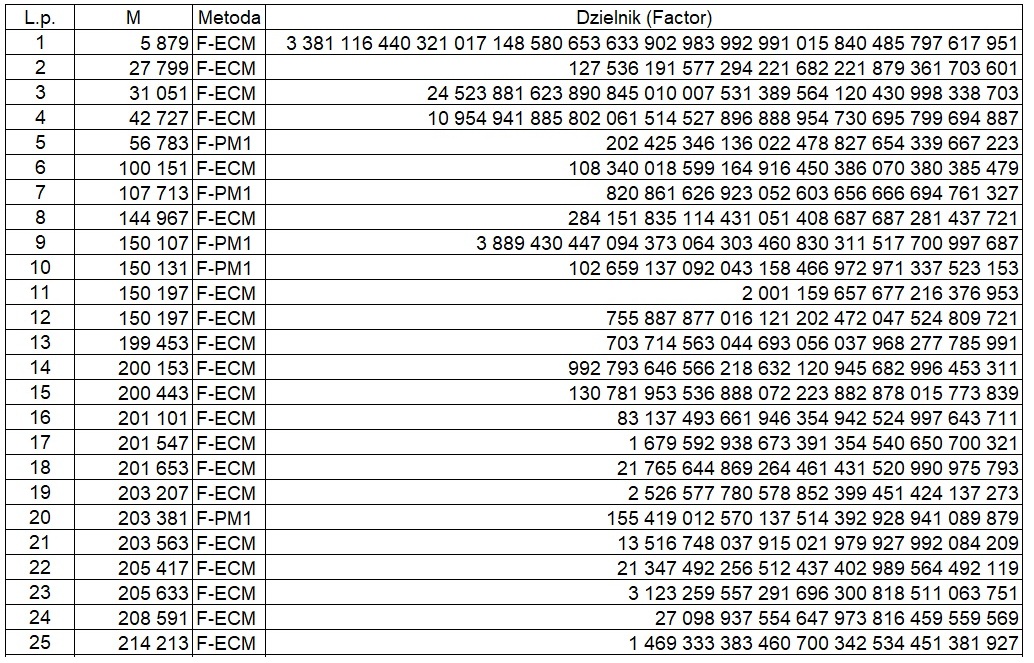
    In the list of the most active users since the beginning of the GIMPS program, I'm ranked sixth of out the 43,973 classified GIMPS participants.
    Below are my best results in the project GIMPS

    Method TF - Trial factoring

    Parameter Mersenne number Factor
    The smallest Mersenne number
    divided by this method    		 M2800951 209976289595486984081 (67,5 bits - 21 digits)
    The biggest Mersenne number
    divided by this method    		 M999997627 3820254763305664277224711 (81,7 bit - 25 digits)
    The smallest factor M5698607 9906451681081561871 (63.1 bits - 19 digits)
    The biggest factor M999997627 3820254763305664277224711 (81,7 bit - 25 digits)

    Other interesting factors found by this method
    Mersenne number Factor
    M103333331 1502212735046366507191 (70,3 bits - 22 digits)
    M103333333 980533203181869656953 (69,7 bits - 21 digits)
    M109777777 37228559200312147915783 (75,0 bits - 23 digits)
    M312020213 (palindrome) 32576289316485929349689 (74,8 bits - 23 digits)
    M373333333 122932898085710697087377 (76,7 bits - 24 digits)
    M444440999 1772485273012075300799 (70,6 bits - 22 digits)
    M737747737 (palindrome containing 3 palindromes - 737 747 737) 44360090772982697051711 (75,2 bits - 23 digits)
    M905696509 (palindrome) 316601093163989338484231 (78,1 bits - 24 digits)
    M919000001 1093595473517132015868497 (79,9 bits - 25 digits)

    Furthermore, for M23243107 I found three factors and what is a peculiarity all three dividers are from one bitlevel TF71.

    Method P-1

    Parameter Mersenne number Factor
    The smallest Mersenne number
    divided by this method    		 M56783 202425346136022478827654339667223 (107,3 bits - 33 digits)
    The biggest Mersenne number
    divided by this method    		 M120012839 121519735251419212169032247 (86,7 bits - 27 digits)
    The smallest factor M4914653 9872797601602413767 (63.1 bits - 19 digits)
    The biggest factor M1105519 2915595290210483905698188678755302313032196817 (151,03 bits - 46 digits)

    Other interesting factors found by this method
    Mersenne number Factor
    M1600061 (palindrome) 3573352964183027918221155860497 (101,5 bits - 31 digits)
    M4441111 16012105959687734439631172715623 (103,7 bits - 32 digits)
    M7079707 (palindrome) 928319223277628296640447231087 (99,6 bits - 30 digits)
    M9918199 (palindrome) 57325434492732146589727793 (85,6 bits - 2digits)
    M1771717 5345322660597600564822049485279823999586101560840103 - composite factor (171,8 bits - 52 digits)

    The largest composite factor 193671015485244594947531289162741682741670915494449569422624338503879 (226.845 bits) = 1073794618247417347831873 * 180361320679128301734184528719388449839439623 for M10290209 has 69 digits.

    Method ECM

    Parameter Mersenne number Factor
    The smallest Mersenne number
    divided by this method    		 M5879 3381116440321017148580653633902983992991015840485797617951 (191.1 bits - 58 digits)
    The biggest Mersenne number
    divided by this method    		 M18012889 13857697029363147737004353 (83.5 bits - 26 digits)
    The smallest factor M1625573 9283472113262929369 (63.0 bits - 19 digits)
    The biggest factor M5879 3381116440321017148580653633902983992991015840485797617951 (191.1 bits - 58 digits)

    Other interesting factors found by this method
    Mersenne number Factor
    M201101 83137493661946354942524997643711 (106,0 bit - 32 cyfry)
    M203207 2526577780578852399451424137273 (101,0 bit - 31 cyfr)
    M1120211 (palindrome) 125280657037737670619618629297 (96,7 bits - 30 digits)
    M1221221 (palindrome) 154473815636202364009228347648751 (106,9 bits - 33 digits)
    M3222223 (palindrome) 1845521789808410044844488439 (90,6 bits - 28 digits)
    M3444443 (palindrome) 964359101168919641266667983 (89,6 bits - 27 digits)
    M3773773 (palindrome) 111560017554966740008537 (76,6 bits - 24 digits)
    M7118117 (palindrome) 9580977160867216251481039 (83,0 bits - 25 digits)
    M11110111 61944963838589697764447441 (85,7 bits - 26 digits)
    M11111119 6652785869722957414101719 (82,5 bits - 25 digits)

    Method P+1

    Parameter Mersenne number Factor
    The smallest Mersenne number divided by this method M2003191 225007102354851248019601430113 (97,5 bits - 30 digits)
    The biggest Mersenne number divided by this method M3000409 36506847546234971967385191137 (94,9 bits - 29 digits)

    counterliczniki